Hàm PPMT
Mục lục
I. Giới thiệu
Các hàm PPMT tính toán phần gốc của một khoản vay với một lịch trình thanh toán cố định và lãi suất.
II. Về hàm
-
Công thức : = PPMT (tỷ_lệ, kỳ, số_kỳ, giá_trị_hiện_tại, [giá_trị_tương_lai], [kết_thúc_hoặc_bắt_đầu])
-
Lập luận :
-
tỷ_lệ (bắt buộc): Lãi suất của khoản vay.
-
kỳ (bắt buộc): Thời hạn thanh toán được đề cập. Nó phải nằm trong khoảng từ 1 đến số_kỳ.
-
số_kỳ (bắt buộc): Tổng số kỳ thanh toán cho khoản vay này.
-
giá_trị_hiện_tại (bắt buộc): Giá trị hiện tại, hoặc tổng giá trị hiện tại của một loạt các khoản thanh toán trong tương lai; còn được gọi là tiền gốc.
-
[giá_trị_tương_lai] (tùy chọn): Giá trị tương lai hoặc số dư tiền mặt bạn muốn nhận sau lần thanh toán cuối cùng. Nếu đối số này bị bỏ qua, thì nó được giả định là 0, nghĩa là giá trị tương lai của khoản vay là 0.
-
[kết_thúc_hoặc_bắt_đầu] (tùy chọn): Các số 0 và 1 thể hiện việc các khoản thanh toán đến hạn vào đầu hay cuối kỳ tương ứng. Nếu bỏ qua, nó được giả định là 0.
-
-
Ví dụ : = PPMT (1%, 1,360,100000,0,0)
-
Lưu ý :
-
Đảm bảo rằng các đơn vị cho lãi suất và số_kỳ là nhất quán. Đối với khoản vay bốn năm với lãi suất 12% được trả hàng tháng, lãi suất phải là 12% / 12 và số_kỳ phải là 4 * 12. Đối với cùng một khoản vay được trả hàng năm, thì lãi suất phải là 12% và số_kỳ phải là 4.
-
III. Các bước
Sử dụng hàm PPMT
-
Chọn một ô và nhập = PPMT .
-
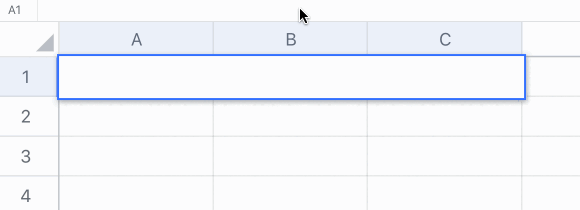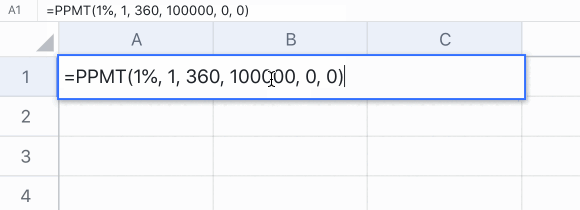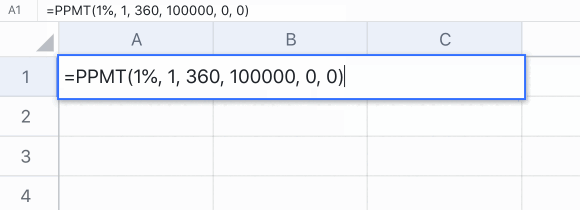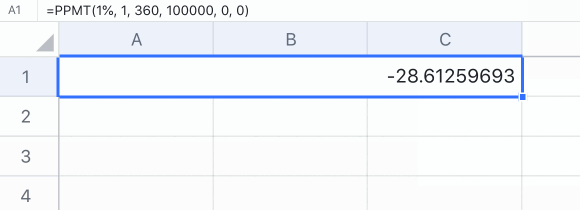
Nhập các đối số trong ô. Ví dụ: = PPMT (1%, 1,360,100000,0,0).
-
Nhấn Enter để có được kết quả, đó là -28.61259693 trong ví dụ này.
Xóa hàm PPMT
Chọn ô có hàm PPMT và nhấn xóa.
IV. Các trường hợp sử dụng
Khoản vay: Tính toán số tiền trả nợ gốc cho một khoảng thời gian cụ thể khoảng thời gian
Đối với các khoản vay thanh toán liên tục mỗi tháng, thanh toán đối với phần gốc tăng dần trong khi phần lãi suất giảm dần. Phép toán có thể khá phức tạp, nhưng hàm PPMT giúp bạn dễ dàng tính toán số tiền trả nợ gốc cho khoảng thời gian quy định.
-
Công thức được sử dụng dưới đây: = PPMT (B2 / 12,1, B3 * 12, B4)
-
Về các đối số:
-
Để chuyển lãi suất hàng năm thành lãi suất hàng tháng, hãy chia cho 12.
-
Để nhận số tiền thanh toán của phần gốc trong tháng đầu tiên, hãy nhập 1.
-
Đối với số_kỳ, chuyển thời hạn thanh toán thành tháng bằng cách nhân thời hạn cho vay, 3, với 12.
-
Chọn B4 làm hiệu trưởng.
-
Nhấn Enter để tìm số tiền trả nợ gốc cho tháng đầu tiên.
-